時間ゆらぎの計算¶
ここでは 時間ゆらぎ (temporal fluctuations) が
(1)![\Avg{
\left[\left(
u_k^i(t) - \Avg{u_k^i(t)}_t
\right)^2 \right]_i
}_{t}
\xrightarrow{N \to \infty}
\sum_l J_{kl}^2 (m_l - q_l)
=
\alpha_k - \beta_k](../../_images/math/3435a1cd9ed7601dc2339b6faa1639d55dca5a8d.png)
となることを示す. [1]
| [1] | 外側の時間平均  は [vanVreeswijk1998]
には無いが,これがあるほうが定義としては自然だろう. 外側の時間平均 は [vanVreeswijk1998]
には無いが,これがあるほうが定義としては自然だろう. 外側の時間平均
 が無くても計算結果は変わらないことは,
時間平均なしでも時間ゆらぎは計算できる で示す. が無くても計算結果は変わらないことは,
時間平均なしでも時間ゆらぎは計算できる で示す. |
まずは  の中身を計算する.
の中身を計算する.
![\left[\left(
u_k^i(t) - \Avg{u_k^i(t)}_t
\right)^2 \right]_i
& \overset{(1)} =
\left[
\sum_{ll'jj'}
J_{kl}^{ij} J_{kl'}^{ij'}
(\sigma_l^j(t) - m_l^j)
(\sigma_{l'}^{j'}(t) - m_{l'}^{j'})
\right]_i
\\
& \overset{(2)} =
\sum_{ll'jj'}
\left[
J_{kl}^{ij} J_{kl'}^{ij'}
\right]_i
(\sigma_l^j(t) - m_l^j)
(\sigma_{l'}^{j'}(t) - m_{l'}^{j'})
\\
& \overset{(3)} \approx
\sum_{lj}
\left[
J_{kl}^{ij} J_{kl}^{ij}
\right]_i
(\sigma_l^j(t) - m_l^j)^2
\\
& \overset{(4)} =
\sum_l
J_{kl}^2
\left(1 - \frac K N_l \right)
\underbrace{
\frac 1 N_l
\sum_j
(\sigma_l^j(t) - m_l^j)^2
}_{(*)}](../../_images/math/23a7d74a535d2d3e57246688c22a11f74880c915.png)
ここで,
(1) 和の積の計算のための添字テクニック,
(2) ニューロンの状態と結合係数の相関 の議論,
(3) 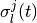 と
と  が無相関なので, 時間平均活動率のゆらぎ と同様に,
が無相関なので, 時間平均活動率のゆらぎ と同様に,
 の項以外は
の項以外は  の大きさしかもたないこと,
(4) 大数の法則 (law of large numbers) と 結合確率の定義 による期待値の計算,
を用いた.
の大きさしかもたないこと,
(4) 大数の法則 (law of large numbers) と 結合確率の定義 による期待値の計算,
を用いた.
この式を時間平均  したものを計算したい. 時間に依存するのは (*) の部分のみなので, これの時間平均をとる.
したものを計算したい. 時間に依存するのは (*) の部分のみなので, これの時間平均をとる.
![\Avg{(*)}_t
& =
\Avg{
\left[
(\sigma_l^j(t) - m_l^j)^2
\right]_j
}_t
\\
& \overset{(1)} =
\Avg{
\left[
\left( \sigma_l^j(t) \right)^2
\right]_j
}_t
-
\left[
(m_l^j)^2
\right]_j
\\
& \overset{(2)} =
\Avg{\PAvg{
\sigma_l^j(t)
}}_t
-
\left[
(m_l^j)^2
\right]_j
\\
& \overset{(3)} =
m_l - q_l](../../_images/math/1c4fa744a1f8f358bb24f88e232502743ae77d02.png)
ここで,
(1) ![[(\Devi x)^2] = [x^2] - [x]^2](../../_images/math/fbc09ca49fb04e28055051285e8f51f5f8fdbcd3.png) と同種の計算,
(2)
と同種の計算,
(2) 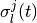 の取りうる値は 0 か 1 なので
の取りうる値は 0 か 1 なので
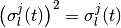 ,
(3)
,
(3) 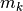 と
と 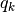 の定義,
を用いた.
の定義,
を用いた.
以上の計算を統合すると,
![\Avg{
\left[\left(
u_k^i(t) - \Avg{u_k^i(t)}_t
\right)^2 \right]_i
}_t
& \approx
\sum_l
J_{kl}^2
\left(1 - \frac K N_l \right)
(m_l - q_l)](../../_images/math/474225f11e191fb94769232f167311098ea3c2a6.png)
が導かれる. これの左辺の極限 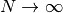 をとると式 (1) が導かれる.
をとると式 (1) が導かれる.
時間平均なしでも時間ゆらぎは計算できる¶
時間に依存する部分 (*) を, 時間平均なしで計算すると

となる.
ただし,  とおいた.
とおいた.
この (*) が定常状態では  と等しいことが示せる. まず,
第一項は
と等しいことが示せる. まず,
第一項は  である. よって, 第三項がゼロになることが示せれば良い.
無相関性の「証明」 の議論から,
である. よって, 第三項がゼロになることが示せれば良い.
無相関性の「証明」 の議論から, 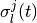 つまり
つまり
 が違うニューロン同士では無相関であることに注意すれば, 無相関変数に対する大数の法則 より,
が違うニューロン同士では無相関であることに注意すれば, 無相関変数に対する大数の法則 より,

となる. これは,

と書ける.
 と
と
 が同じ (集団レベルでの, あるいはグローバルな) 量を違う時間で評価したものであることを考慮すれば, 定常状態ではこの量は時間に依らないはずであり,
が同じ (集団レベルでの, あるいはグローバルな) 量を違う時間で評価したものであることを考慮すれば, 定常状態ではこの量は時間に依らないはずであり,  が導ける.
が導ける.
もっと形式的にこれを導出するためには, 自己相関関数

を使う. これを用いれば,

となることが導ける. ただし, (1) で系が定常状態にあると自己相関関数が時間差のみに依存すること  を用い, (2) で時間平均が時間シフトの元で不変であることを用いた
を用い, (2) で時間平均が時間シフトの元で不変であることを用いた