クエンチされたゆらぎの計算¶
ここでは, クエンチされたゆらぎ (quenched fluctuations) [1] が
(1)![\left[ \left( \Devi \Avg{u_k^i(t)}_t \right)^2 \right]
\xrightarrow{N \to \infty}
\sum_{l=1,2} J_{kl}^2 q_l =: \beta_k](../../_images/math/115c0b9305857833f2e6e63f65a79deaf2763af4.png)
となることを示す. ただし,  は長い時間にわたる平均である.
ここで,
は長い時間にわたる平均である.
ここで, 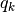 は オーダーパラメター (order parameter)
と呼ばれ, ニューロン
は オーダーパラメター (order parameter)
と呼ばれ, ニューロン 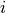 の活動率の時間平均
の活動率の時間平均 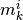 を用いて,
を用いて,

と定義される.
| [1] | 無理やり日本語にすると「焼入れされたゆらぎ」と言うのだろうか. |
偏差の分解¶
まず,  の集団平均
の集団平均 ![[\Avg{u_k^i(t)}_t]](../../_images/math/319abbc7883182835e67814972094c2ecb75cba4.png) からのズレ具合 (偏差) を次のように, 2つの成分に分解できることを示す.
からのズレ具合 (偏差) を次のように, 2つの成分に分解できることを示す.

ここで (d1) は 「結合数のゆらぎ」, (d2) [2] は 「時間平均活動率のゆらぎ」である. 結合数は時間によらないので, そのゆらぎが「クエンチされている」のは当然であるが, 活動率の時間平均  も
(平均操作のおかげで) 時間によらないので, そのゆらぎもクエンチされたゆらぎに含める必要がある. つまり,
クエンチされたゆらぎのうち, 直接の影響である (d1) 「結合数のゆらぎ」と, それが引き起こす間接的な影響である (d2) 「時間平均活動率のゆらぎ」の2つを勘定すれば良い, という主張である.
も
(平均操作のおかげで) 時間によらないので, そのゆらぎもクエンチされたゆらぎに含める必要がある. つまり,
クエンチされたゆらぎのうち, 直接の影響である (d1) 「結合数のゆらぎ」と, それが引き起こす間接的な影響である (d2) 「時間平均活動率のゆらぎ」の2つを勘定すれば良い, という主張である.
| [2] | ここでの (d1) は, 原著 [vanVreeswijk1998] の式(5.5)
と同値であることは, |
これは, 地道に入力の時間平均  の偏差を計算することによって示せる:
の偏差を計算することによって示せる:
![\Devi \Avg{u_k^i(t)}_t
& \overset{(1)} =
\Devi \Avg{
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t)
}_t
\\
& \overset{(2)} =
\Devi \left(
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} m_l^j
\right)
\\
& \overset{(3)} =
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} m_l^j
-
\left[
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{i'j} m_l^j
\right]_{i'}
\\
& \overset{(4)} =
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} m_l^j
-
\sum_{l = E, I} [J_{kl}^{i'j'}]_{i'} \sum_{j=1}^{N_l} m_l^j
\qquad (\forall j')
\\
& \overset{(5)} \approx
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} m_l^j
-
\underbrace{
\sum_{l = E, I} [J_{kl}^{i'j'}]_{i'} \sum_{j=1}^{N_l} m_l
}_{\text{nothing depends on } j}
\\
& \overset{(6)} =
\sum_{l = E, I} \sum_{j=1}^{N_l}
\left\{
J_{kl}^{ij} (m_l^j - m_l)
- (J_{kl}^{ij} - [J_{kl}^{i'j'}]_{i'}) m_l
\right\}
\\
& =
\text{(d1)} + \text{(d2)}](../../_images/math/fad8c8d93e458410bf24c8a52d1849689e2043e1.png)
ここで,
(1)  ,
(2) 定義
,
(2) 定義  ,
(3) 偏差
,
(3) 偏差 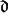 の定義,
(4) ニューロンの状態と結合係数の相関 の議論,
(5)
の定義,
(4) ニューロンの状態と結合係数の相関 の議論,
(5) ![\sum_{j=1}^{N_l} m_l^j = N_l N_l^{-1} \sum_{j=1}^{N_l} m_l^j
= N_l [m_l^{j''}]_{j''} = N_l m_l](../../_images/math/dc12a36e72de50e8ecbb647796c94a733f7b27cb.png) であり,
であり,  なので, 結局
なので, 結局  ,
(6)
,
(6)  ,
を用いた.
式変形 (4) の右辺とそれ以降の式中に現れる
,
を用いた.
式変形 (4) の右辺とそれ以降の式中に現れる  は,
は,  から
から  のどの値をとっても良い. これは 大数の法則 (law of large numbers) より
のどの値をとっても良い. これは 大数の法則 (law of large numbers) より ![[J_{kl}^{i'j'}]_{i'}](../../_images/math/0c7d5ece1fcd44f0995b84b1d39b66d6b164b6ee.png) が同じ値に収束するからである.
が同じ値に収束するからである.
ふたつの偏差の相関¶
上記の計算より導かれた2つの偏差の二乗平均をとって, ゆらぎを
![\left[
\left(
\Devi \Avg{u_k^i(t)}_t
\right)^2
\right]
=
\left[
\text{(d1)}^2
\right]
+
\left[
\text{(d2)}^2
\right]](../../_images/math/482593a99912c94f957d92d0945a483112b379fc.png)
のように求めたいが, そのためにはそれらの偏差が無相関  でなければならない. これは簡単に示せる:
でなければならない. これは簡単に示せる:
![&
\left[
\text{(d1)}
\text{(d2)}
\right]
\\
& \overset{(1)} =
\left[
\sum_{ll'jj'}
\Devi J_{kl}^{ij} \, m_l \,
J_{kl'}^{ij'} \, \Devi m_{l'}^{j'}
\right]_i
\\
& \overset{(2)} =
\sum_{ll'jj'}
\left[
\Devi J_{kl}^{ij} \, J_{kl'}^{ij'}
\right]_i
m_l \, \Devi m_{l'}^{j'}
\\
& \overset{(3)} =
\sum_{lj}
\left(
\left[(J_{kl}^{i*})^2 \right]_i
-
\left[J_{kl}^{i*} \right]_i^2
\right)
m_l \, \Devi m_{l'}^{j}
\\
& =
\sum_{l}
\left(
\left[(J_{kl}^{i*})^2 \right]_i
-
\left[J_{kl}^{i*} \right]_i^2
\right)
m_l \,
\underbrace{\sum_j \Devi m_{l'}^{j}}_{=0}
\\
& = 0](../../_images/math/593f735de5ffbaab3207b48d2820b49a324b09fa.png)
式変形 (1) では ニューロンの状態と結合係数の相関 の議論を用いた.
式変形 (2) では,
![\left[\Devi J_{kl}^{ij} \, J_{kl'}^{ij'} \right]_i](../../_images/math/38a5931784f21a71f31dd67b640ae124fd434003.png) は
は  だと
だと
![\left[\Devi J_{kl}^{ij} \, J_{kl'}^{ij'} \right]_i
=
\left[ \Devi J_{kl}^{ij} \right]_i
\left[ J_{kl'}^{ij'} \right]_i
= 0](../../_images/math/d2cc5ef94b488f178cc4e46eb43260d373e6e8ae.png)
なので, 非ゼロになるのは  の場合のみであることを用いた.
式変形 (3) は, 偏差
の場合のみであることを用いた.
式変形 (3) は, 偏差 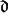 の定義に沿って
の定義に沿って
![\left[\Devi J_{kl}^{ij} \, J_{kl}^{ij} \right]_i
=
\left[ (J_{kl}^{ij})^2 \right]_i
-
\left[ J_{kl}^{ij} \right]_i^2](../../_images/math/8fcff493aa2f0d0b7ec2f9db466cea25b9637d00.png)
という計算をすれば良い. 式変形 (3) の右辺以降に現れる添字の  は, この部分の添字が何でも良いことを表す.
は, この部分の添字が何でも良いことを表す.
結合数のゆらぎ¶
![[\text{(d1)}^2]
& =
\left[ \left(
\sum_l \sum_j \Devi J_{kl}^{ij} \, m_l
\right)^2 \right]_i
\\
& \overset{(1)} =
\left[
\sum_{ll'jj'}
\Devi J_{kl}^{ij} \, \Devi J_{kl'}^{ij'}
\, m_l \, m_{l'}
\right]_i
\\
& \overset{(2)} =
\sum_{ll'jj'}
\left[
\Devi J_{kl}^{ij} \, \Devi J_{kl'}^{ij'}
\right]_i
m_l \, m_{l'}
\\
& \overset{(3)} =
\sum_j
J_{kl}^2 \left(1 - \frac K N_l \right)
\left( m_l \right)^2](../../_images/math/1e1d95554be69f7d5921e4a2d513c460f7f46cb1.png)
ここで,
(1) 和の積の計算のための添字テクニック と
(2) ニューロンの状態と結合係数の相関 の議論を用いた.
最後の式変形 (3) では,
 だと
だと
![\left[
\Devi J_{kl}^{ij} \, \Devi J_{kl'}^{ij'}
\right]_i
=
\left[
\Devi J_{kl}^{ij}
\right]_i
\left[
\Devi J_{kl'}^{ij'}
\right]_i
= 0](../../_images/math/7d198f063ed66add71683c42779e0ebd2dcd7c4a.png)
となり,
 だと
だと
![\left[\left(
\Devi J_{kl}^{ij}
\right)^2 \right]_i
& \overset{(1)} =
\left[\left(
J_{kl}^{ij}
\right)^2 \right]_i
-
\left( \left[
J_{kl}^{ij}
\right]_i \right)^2
\\
& \overset{(2)} \approx
\left(
\frac{J_{kl}}{\sqrt K}
\right)^2
\frac{K}{N_l}
-
\left(
\frac{J_{kl}}{\sqrt K}
\frac{K}{N_l}
\right)^2
\\
& =
\frac{J_{kl}^2}{N_l}
\left(
1 - \frac{K}{N_l}
\right)](../../_images/math/cdb68dfb76e3d1d239a2c2dac8eb7aebabfc1ea1.png)
となることを用いた.
この計算では,
(1) 偏差 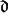 の定義を使い,
(2) 大数の法則 (law of large numbers) と 結合確率の定義 による期待値の計算をした.
の定義を使い,
(2) 大数の法則 (law of large numbers) と 結合確率の定義 による期待値の計算をした.
時間平均活動率のゆらぎ¶
![[\text{(d2)}^2]
& =
\left[ \left(
\sum_l \sum_j J_{kl}^{ij} \, \Devi m_l^j
\right)^2 \right]_i
\\
& \overset{(1)} =
\left[
\sum_{ll'jj'}
J_{kl}^{ij} \, J_{kl'}^{ij'}
\Devi m_l^j \, \Devi m_{l'}^{j'}
\right]_i
\\
& \overset{(2)} \approx
\sum_{ll'jj'}
\left[
J_{kl}^{ij} \, J_{kl'}^{ij'}
\right]_i
\Devi m_l^j \, \Devi m_{l'}^{j'}
\\
& =
\sum_{\substack{ll' \\ l \neq l'}}
\sum_{jj'}
\bullet
+
\sum_l
\sum_{\substack{jj' \\ j \neq j'}}
\bullet
+
\sum_l
\sum_j
\bullet](../../_images/math/0826aa7821afd078b6ee0f8a7a9a1d88911cc7ab.png)
ここで, (1) 和の積の計算のための添字テクニック と (2) ニューロンの状態と結合係数の相関 の議論を用いた. 上記の3つの項は以下のように計算できる.
![\sum_{\substack{ll' \\ l \neq l'}}
\sum_{jj'}
\left[
J_{kl}^{ij} \, J_{kl'}^{ij'}
\right]_i
\Devi m_l^j \, \Devi m_{l'}^{j'}
& =
\sum_{\substack{ll' \\ l \neq l'}}
\left[J_{kl}^{i*} \, J_{kl'}^{i*} \right]_i
\sum_j \Devi m_l^j
\sum_{j'} \Devi m_{l'}^{j'}
= 0](../../_images/math/7ba31252995250657ebbcfb189a8cd06b07b5131.png)
![\sum_l
\sum_{\substack{jj' \\ j \neq j'}}
\left[
J_{kl}^{ij} \, J_{kl'}^{ij'}
\right]_i
\Devi m_l^j \, \Devi m_{l'}^{j'}
& =
\sum_l
\left[J_{kl}^{i*} \right]_i^2
\sum_j \Devi m_l^j
\sum_{\substack{j' \\ j \neq j'}} \Devi m_l^{j'}
\\
& \overset{(1)} =
\sum_l
\left(
\frac{J_{kl}}{\sqrt K}
\frac{K}{N_l}
\right)^2
\sum_j \Devi m_l^j
\left(
\sum_{j'} \Devi m_l^{j'} - \Devi m_l^j
\right)
\\
& =
K
\sum_l
(J_{kl})^2
\frac{1}{N_l}
\sum_j \Devi m_l^j
\left(
\frac{1}{N_l} \sum_{j'} \Devi m_l^{j'}
-
\frac{1}{N_l} \Devi m_l^j
\right)
\\
& \overset{(2)} =
K
\sum_l
(J_{kl})^2
\left(
[\Devi m_l^j]_j
[\Devi m_l^{j'}]_{j'}
-
\frac{1}{N_l}
[(\Devi m_l^j)^2]_j
\right)
\\
& \overset{(3)} =
O(K/N)](../../_images/math/064ff968ac5f4f6023fc8567abf0596651ed04e2.png)
ここで,
(1) 結合確率の定義 による期待値の計算,
(2) 集団平均の定義  ,
(3)
,
(3) ![[\Devi m_l^j]_j = 0](../../_images/math/9d1c9d7df085993b4093c263a12e4b328fab6a81.png) を用いた
を用いた
![\sum_l
\sum_j
\left[
(J_{kl}^{ij})^2
\right]_i
(\Devi m_l^j)^2
& \overset{(1)} =
\sum_l
\left[
(J_{kl}^{i*})^2
\right]_i
N_l
\left[
(\Devi m_l^j)^2
\right]_j
\\
& \overset{(2)} =
\sum_l
\left(
\frac{J_{kl}}{\sqrt K}
\right)^2
\frac{K}{N_l}
N_l
\left[
(\Devi m_l^j)^2
\right]_j
\\
& =
\sum_l
J_{kl}^2
\left[
(\Devi m_l^j)^2
\right]_j
\\
& \overset{(3)} =
\sum_l
J_{kl}^2
\left(
[(m_l^j)^2] - [m_l^j]^2
\right)
\\
& \overset{(4)} =
\sum_l
J_{kl}^2
\left(
q_l - m_l^2
\right)](../../_images/math/55c5d014e7ad90ca89674426e9e3ecad3714bbb2.png)
ここで,
(1) ![\left[(J_{kl}^{ij})^2 \right]_i](../../_images/math/3604fdebe8b0d7442762055a6c3cbbf21f6649ed.png) が
が 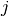 に依存しないこと,
(2) 大数の法則 (law of large numbers) と 結合確率の定義 による期待値の計算,
(3)
に依存しないこと,
(2) 大数の法則 (law of large numbers) と 結合確率の定義 による期待値の計算,
(3) ![[(\Devi x)^2] = [x^2] - [x]^2](../../_images/math/fbc09ca49fb04e28055051285e8f51f5f8fdbcd3.png) ,
(4)
,
(4) 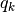 と
と 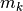 の定義を用いた.
の定義を用いた.
![\delta_1 \langle u_k^i \rangle
= \sum_{l=1}^2 \sum_{j=1}^{N_l} \delta J_{kl}^{ij} [m_l^j]](../../_images/math/f46b702c408d08866743ada5d56b1da5e1d98026.png)
![[m_l^j] = m_l](../../_images/math/976049832c81e3dedd590892487c4e5545714bdd.png) より分かる.
しかし, この表記では,
より分かる.
しかし, この表記では, ![[m_l^j]](../../_images/math/09a0e15cce51714b1b512b213e4a54cb0687266f.png) が何を意味する不鮮明である.
親切に書くのならば,
が何を意味する不鮮明である.
親切に書くのならば, ![[m_l^{j'}]_{j'}](../../_images/math/f2785cd99b7327d6477716e124425e609e90ba45.png) として,
集団平均が添字
として,
集団平均が添字 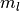 と書く方が良い.
と書く方が良い.![\left[
\left(
\Devi \Avg{u_k^i(t)}_t
\right)^2
\right]
& \approx
\left[
\text{(d1)}^2
\right]
+
\left[
\text{(d2)}^2
\right]
\\
& \approx
\sum_j
J_{kl}^2 \left(1 - \frac K N_l \right)
\left( m_l \right)^2
+
\sum_l
J_{kl}^2
\left(
q_l - m_l^2
\right)
\\
& =
\sum_l J_{kl}^2 \, q_l
+ O(N_l^{-1})
\\
& \xrightarrow{N \to \infty}
\sum_l J_{kl}^2 \, q_l](../../_images/math/d9ce35e18709fa89442c1bba48b9c29d71117939.png)