秩序変数の計算¶
これまでの計算で, クエンチされたゆらぎ(空間ゆらぎ)と時間ゆらぎを集団平均活動率 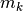 と秩序変数
と秩序変数 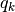 で表すことが出来ると分かったが, 秩序変数
で表すことが出来ると分かったが, 秩序変数 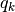 の計算方法がまだ分からないので, これでは答えを得たとは言えない.
ここでは, 秩序変数
の計算方法がまだ分からないので, これでは答えを得たとは言えない.
ここでは, 秩序変数 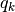 が満たすべき関係式
(自己無頓着 (self-consistent) 方程式)
を導く.
が満たすべき関係式
(自己無頓着 (self-consistent) 方程式)
を導く.
平均場方程式の導出 と同様に, ニューロンの状態
 を標準ガウス確率変数で書きなおそう. 今度は, 入力
を標準ガウス確率変数で書きなおそう. 今度は, 入力 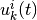 のゆらぎをクエンチされたゆらぎ(空間ゆらぎ)と時間ゆらぎをに分け,
それぞれ独立な標準ガウス確率変数
のゆらぎをクエンチされたゆらぎ(空間ゆらぎ)と時間ゆらぎをに分け,
それぞれ独立な標準ガウス確率変数 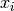 と
と  で表す. [1]
つまり, 確率変数
で表す. [1]
つまり, 確率変数 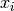 と
と  は
は
 と
と
 を満たすとする. これらの確率変数を用いて入力を
を満たすとする. これらの確率変数を用いて入力を

と書いて実数  を求めよう.
クエンチされたゆらぎの計算 の結果と
を求めよう.
クエンチされたゆらぎの計算 の結果と
![\left[ \left( \Devi \Avg{u_k^i(t)}_t \right)^2 \right]
=
\left[ \left( \Devi (c x_i) \right)^2 \right]
=
\left[ \left( c x_i \right)^2 \right]
=
c^2](../../_images/math/a2393c884b25a8f1acd078a4236ae9ab4db5ef36.png)
より,  ,
時間ゆらぎの計算 の結果と
,
時間ゆらぎの計算 の結果と
![\Avg{
\left[\left(
u_k^i(t) - \Avg{u_k^i(t)}_t
\right)^2 \right]_i
}_{t}
=
\Avg{
\left[\left(
d y_i(t)
\right)^2 \right]_i
}_{t}
=
d^2](../../_images/math/e7c4a9b24dc5ac1b5b1b42658dcc95a0497969b7.png)
より,  が言える.
が言える.
| [1] | 確率変数 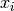 とある時間 とある時間 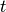 における時間ゆらぎ成分を表す確率変数 における時間ゆらぎ成分を表す確率変数  は独立だが,
違う時間 は独立だが,
違う時間  と比べて, と比べて,  と と
 が独立, という意味では ない.
確率変数 が独立, という意味では ない.
確率変数  と と  はもちろん相関を持ち, その相関構造は はもちろん相関を持ち, その相関構造は 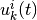 の自己相関関数を計算することで理解できる. の自己相関関数を計算することで理解できる. |
よって, ニューロンの状態
 は
は

と書けることが分かった.
この表式では, 時間平均  は確率変数
は確率変数  に関する平均と同値
(つまり,
に関する平均と同値
(つまり,  )
なので,
)
なので,  は
は
(1)
と書ける. この表式を用いて  を計算すると,
を計算すると,
(2)
となる. クエンチされたゆらぎ  が
が 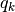 に依存していることを思い出せば, この式は秩序変数
に依存していることを思い出せば, この式は秩序変数 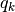 が満たすべき関係式であり,
が満たすべき関係式であり, 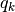 を陰に定義していることが分かる.
を陰に定義していることが分かる.
時間ゆらぎが無い場合
 :
: は
は  に依存しないので,
に依存しないので,
 [2] となるから,
[2] となるから,  より,
より,
である. 時間ゆらぎの計算 で導いた関係式より,
 となり, 時間ゆらぎが無いという仮定と整合性があるので,
となり, 時間ゆらぎが無いという仮定と整合性があるので,
 は式 (2) の解のひとつである. この解を, 原著 [vanVreeswijk1998] にならい
凍結解 (frozen solution) と呼ぶ.
時間ゆらぎは二乗の平均なので正, つまり
は式 (2) の解のひとつである. この解を, 原著 [vanVreeswijk1998] にならい
凍結解 (frozen solution) と呼ぶ.
時間ゆらぎは二乗の平均なので正, つまり
 は正である.
は正である.また,
 より, 各点
より, 各点 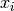 で
で
 だから,
だから,
 ,
つまり凍結解
,
つまり凍結解  は秩序変数
は秩序変数 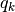 の上限を与えることが分かる.
の上限を与えることが分かる.[2] クエンチされたゆらぎがない場合
 :
:式 (2) に
 を代入すると,
を代入すると,
 は
は 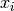 に依存しなくなり,
に依存しなくなり,
となる. しかし, クエンチされたゆらぎの計算 で求めた関係式
 にこれをあてはめると,
にこれをあてはめると,
 または
または  というトリビアルな状況を除けば,
というトリビアルな状況を除けば,  となり, 仮定
となり, 仮定  とは整合性がとれない. よって,
とは整合性がとれない. よって,  は解ではない.
一方で, イェンゼンの不等式 (Jensen’s inequality) [3] を用いれば,
は解ではない.
一方で, イェンゼンの不等式 (Jensen’s inequality) [3] を用いれば,
 , つまりクエンチされたゆらぎがない場合
, つまりクエンチされたゆらぎがない場合  が秩序変数
が秩序変数 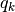 の下限を与えることが分かる.
の下限を与えることが分かる.[3] (下に)凸関数
 と
と 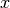 に関する平均
に関する平均 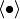 について,
について,  が成り立つ. これを,
イェンゼンの不等式 (Jensen’s inequality) という.
参考: イェンゼンの不等式 - Wikipedia
/
Jensen’s inequality - Wikipedia
が成り立つ. これを,
イェンゼンの不等式 (Jensen’s inequality) という.
参考: イェンゼンの不等式 - Wikipedia
/
Jensen’s inequality - Wikipedia
 は,
は,  の場合の
の場合の  でもある.
でもある.